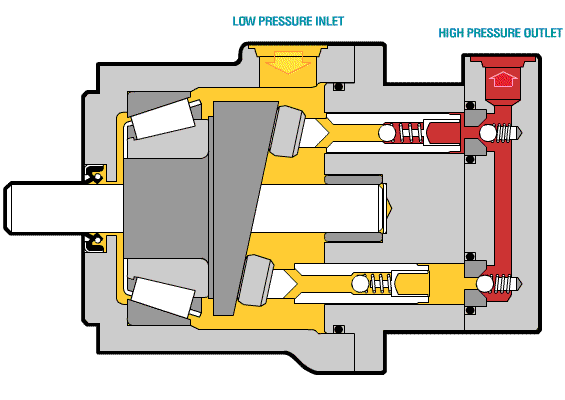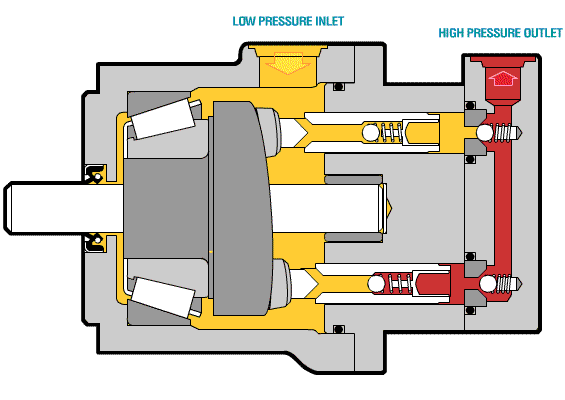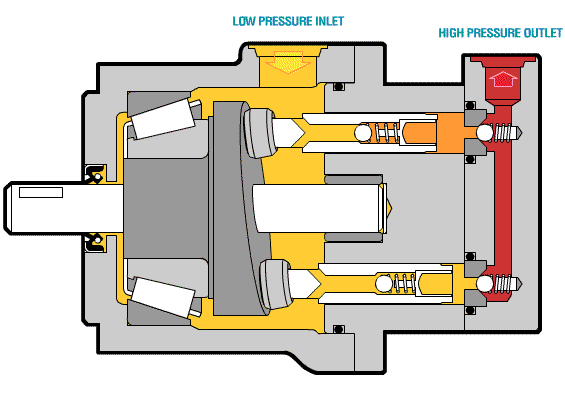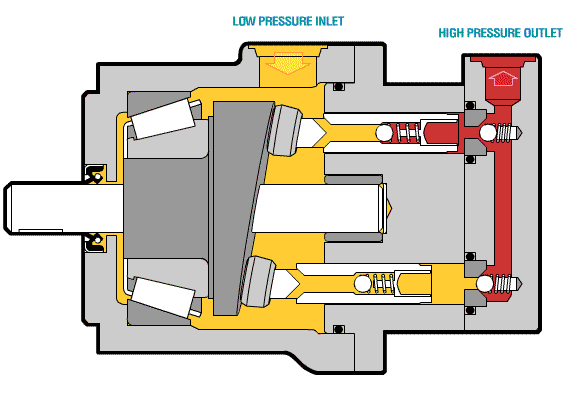
Việc áp dụng Phương Trình Euler vào Máy Bơm Hướng Trục không chỉ đơn thuần là việc rút gọn công thức; nó mở ra một thách thức kỹ thuật quan trọng liên quan đến sự phân bố áp suất và tốc độ dọc theo bán kính (r) của BXCT. Với điều kiện dòng chảy theo mặt hình trụ, vận tốc kéo theo (U) sẽ tăng tuyến tính theo bán kính (U=ω⋅r). Theo công thức Euler rút gọn (H−1=gU⋅C2u), nếu các thông số khác không đổi, cột nước sẽ lớn hơn ở ngoại vi so với ở gần tâm.
Bài viết chuyên sâu này sẽ tập trung vào phân tích toán học và ứng dụng kỹ thuật của Phương trình Euler cho bơm hướng trục (Công thức 3-13). Chúng ta sẽ chứng minh tại sao cột nước càng xa tâm càng lớn và từ đó đưa ra chiến lược thiết kế cánh để đạt được mục tiêu quan trọng nhất: Cân Bằng Cột Nước Toàn Phần (H) đồng đều trên toàn bộ cánh bơm (Ha=Hb). Giải pháp kỹ thuật then chốt là phải điều chỉnh thành phần vận tốc tiếp tuyến (C2u) bằng cách thay đổi góc cánh (β2) theo bán kính.
Rút Gọn Phương Trình Euler và Nhận Xét Cơ Bản
- 1.1. Điều Kiện Rút Gọn:
- Dòng chảy là hình trụ: r1=r2=r.
- Vận tốc kéo theo: U1=U2=U=ω⋅r.
- Giả thiết lý tưởng không có xoáy vào: C1u=0.
- 1.2. Công Thức Rút Gọn (Công thức 3-13):
- Phương trình cơ bản của bơm hướng trục lý tưởng:
H−1=gU⋅C2u
- 1.3. Vấn Đề Về Tính Đồng Nhất Dọc Bán Kính:
- Ta thấy H−1 tỷ lệ thuận với U, và U tỷ lệ thuận với r.
- Nhận xét: Nếu giả sử thành phần C2u giữ không đổi theo bán kính (r), thì cột nước càng xa tâm sẽ càng lớn.
- Ví dụ (Hình 3-4): Xét hai mặt cắt a (gần tâm) và b (xa tâm). Do Ub>Ua, ta có:
Hb=gUb⋅C2u>Ha=gUa⋅C2u
-
- Sự phân bố cột nước không đồng đều này là không mong muốn vì nó làm giảm hiệu suất và gây ra áp lực không đối xứng.
Chiến Lược Cân Bằng Cột Nước H Toàn Cánh (Ha=Hb)
- 2.1. Mục Tiêu Kỹ Thuật:
- Trong thiết kế bơm hướng trục, mục tiêu là đảm bảo cột nước toàn phần (H) bằng nhau trên toàn bộ cánh bơm, tức là H(r)=ha˘ˋng soˆˊ.
- 2.2. Điều Chỉnh C2u Theo r:
- Để Ha=Hb, do Ub>Ua, từ công thức H−1=gU⋅C2u, ta phải điều chỉnh:
C2u∝U1∝r1
-
- Kết luận: Thành phần vận tốc tiếp tuyến C2u phải giảm dần từ tâm ra ngoại vi để bù đắp cho sự tăng của vận tốc kéo theo U.
- 2.3. Điều Kiện Về Lưu Lượng Đồng Đều:
- Ngoài ra, để đảm bảo lưu lượng (Q) đi qua đồng đều tại mọi bán kính, thành phần vận tốc hướng trục (hướng kính) C2r phải được giữ gần như không đổi (C2r,a=C2r,b) (xem tam giác tốc độ cửa ra – Hình 3-8).
Phân Tích Tam Giác Tốc Độ và Góc Cánh (β2)
- 3.1. Phụ Thuộc Của C2u vào β2:
- Trong tam giác tốc độ cửa ra (Hình 3-8), thành phần C2u phụ thuộc trực tiếp vào góc cánh ra β2 (góc giữa W2 và U2) và thành phần C2r:
C2u=U2−W2u=U2−tanβ2C2r
- 3.2. Điều Kiện Thay Đổi Góc Cánh:
- Ta có: U tăng theo r và C2u phải giảm theo r.
- Xét tại tâm (ra): Ua nhỏ, C2u,a lớn. Để C2u,a lớn, góc β2a phải lớn (làm cho W2u nhỏ).
- Xét tại ngoại vi (rb): Ub lớn, C2u,b nhỏ. Để C2u,b nhỏ, góc β2b phải nhỏ (làm cho W2u lớn).
- 3.3. Kết Luận Về Hình Dạng Cánh:
- Vì β2a phải lớn hơn β2b (β2a>β2b), nên ta thấy cánh bơm hướng trục phải được chế tạo có góc nghiêng nhỏ dần từ trong ra ngoài (từ tâm ra ngoại vi).
Ảnh Hưởng Dòng Chảy và Ứng Dụng Thực Tiễn
- 4.1. Tối Ưu Hóa Hiệu Suất:
- Việc thiết kế BXCT với góc cánh xoắn (Twisted Blade) theo bán kính không chỉ đảm bảo H đồng đều mà còn tối ưu hóa luồng chảy, giảm thiểu tổn thất do xoáy và đảm bảo hiệu suất cao nhất trong dải lưu lượng lớn.
- 4.2. Khó Khăn Trong Chế Tạo:
- Thiết kế cánh xoắn (twisted) là một thách thức lớn trong chế tạo bơm hướng trục. Cánh phải được đúc hoặc gia công cơ khí chính xác để đảm bảo biên dạng và góc nghiêng chính xác tại mọi điểm trên bán kính. Sai lệch nhỏ có thể dẫn đến phân bố áp lực không đều và rung động khi vận hành.
- 4.3. Ứng Dụng Thực Tiễn:
- Các bơm hướng trục được sử dụng phổ biến trong các trạm bơm thủy lợi lớn, hệ thống thoát nước đô thị và hệ thống tuần hoàn nước làm mát công suất cao, nơi yêu cầu cung cấp lưu lượng khổng lồ với cột nước thường dưới 10m.
Việc áp dụng Phương trình Euler cho Bơm Hướng Trục (dạng H−1=gU⋅C2u) cho thấy một thách thức kỹ thuật lớn: cột nước có xu hướng tăng theo bán kính. Để đạt được mục tiêu cân bằng cột nước (H) đồng đều trên toàn bộ cánh bơm và duy trì lưu lượng ổn định, các chuyên gia phải thiết kế sao cho thành phần vận tốc tiếp tuyến (C2u) giảm tỷ lệ nghịch với bán kính (r). Điều này dẫn đến yêu cầu bắt buộc: cánh bơm hướng trục phải có góc nghiêng (β2) nhỏ dần từ tâm ra ngoại vi (β2a>β2b), đây là một đặc điểm thiết kế then chốt của loại bơm hiệu suất cao này.